For example, when reflecting the point (2,5) over y=x it becomes (5,2) This is very simple, but why does it work?A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (2, 2), B (6, 5) and C (3, 6) Triangle DEF has vertices D (2, 2), E (5, 6), and F (6, 3) This concept is new to me I am doing a university level class and the way this class is presented is very theoretical that I even struggle to read
Reflection Over The Line Y X Math Showme
Y=x line reflection
Y=x line reflection-The point located (3,1) is reflected across the yaxisWhat are the coordinates of the reflected p The point A (7,5) is reflected over the line x=5 and then is reflected over the line x=2 what are The point A (3, 4) is reflected over the line x = 2, and then is reflected over the line x= 4A reflection of the point across the xaxis a reflection of the point across the yaxis a reflection of the point across the line y = x a reflection of the point across the line y = x Click card to see definition 👆




D Reflection Across Y X Brainly Com
or y = x (2, 2) (4, 4) (5, 5) Just plotting a few of these coordinates will make sure that you always reflect in the correct mirror line The only other issue is to make sure that your reflection is at 90 degrees to the line, and it's the same distance both sides Other than that, you're good to go Here's some videos to helpThis is a KS3 lesson on reflecting a shape in the line y = x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendableYou can use a formula When you reflect over xaxis the coordinates are (x,y) and when you reflect over the yaxis the coordinates are (x,y If you want to reflect over y=x then the coordinates are (y,x) If you want to reflect over y=x the coordinates are (y,x) Comment on Caylen Jang's post "You can use a formula
To reflect along a line that forms an angle θ with the horizontal axis is equivalent to rotate an angle − θ (to make the line horizontal) invert the y coordinate rotate θ back Further, y = mx implies tanθ = m, and 1 m2 = 1 cos2θ Then, assumming you know about rotation matrices, you can writeBig Ideas A function maps a set of inputs (a domain) to a set of outputs (a range), and each element of the domain is related to exactly one element of the range An inverse of a function maps the outputs back to their corresponding inputs, and hence the range of a function is the domain of the inverse The graph of an inverse of a function is a reflection of the function across the line y=xHow To Given a function, reflect the graph both vertically and horizontally Multiply all outputs by –1 for a vertical reflection The new graph is a reflection of the original graph about the xaxis Multiply all inputs by –1 for a horizontal reflection The new graph is a reflection of the original graph about the yaxis
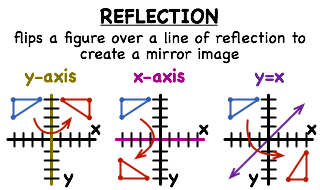
The triangles are reflected across the line y = –x Answers 2 Show answers Another question on Mathematics Mathematics, 1410 Will give brainliest series to sigma notation write the following series in sigma notation example image shown below Answers 1What is a Reflection? A reflection of a point, a line, or a figure in the X axis involved reflecting the image over the x axis to create a mirror image In this case, the x axis would be called the axis of reflection Math Definition Reflection Over the Y Axis




Reflections Through The Axes And The Lines Y X And Y X Geogebra




Picture Of Reflection Across Y Axis Reflection Math Reflection Math
Reflection in the line y = x A reflection of a point over the line y = x is shown The rule for a reflection in the line y = x is ( x , y ) → ( y , x )Reflection about the line y = x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure Let us consider the following example to have better understanding of reflection14 Reflections Over y = x, y = –x, y = #, & x = # Geometry Directions Write the rule of the transformation (This is a mixed review) 1) A line segment is reflected over y = –x 2) A line segment is translated 5 units left & 1 unit up




Reflections Ck 12 Foundation




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
Key Points A vertical reflection is given by the equation y=−f (x) y = − f (x) and results in the curve being "reflected" across the xaxis A horizontal reflection is given by the equation y=f (−x) y = f (− x) and results in the curve being "reflected" across the yaxis Other Lines A reflection can occur across any line, it is not limited to the three lines discussed previously The example below demonstrates a reflection that is not specific to the axes or the line y = x Examine the drawing below to see the relationship between the coordinates of the preimage and imageCheck all that apply 1 Every line connects two vertices 2Every line connects the midpoints of 2 sides 3Every line bisects a vertex angle 4Every line bisects a side 5Every line is perpendicular to a side 3 Every line bisects a vertex angle 4 Every line bisects a side 5 Every line is perpendicular to a side



Answered Rules For Reflections On A Coordinate Bartleby




Algebraic Representations Of Reflections
The x and y units of your graph is not balanced anymore, the line y=x does not have an angle of 45 degrees, so what do you expect then – user May 18 '19 at 622 I actually wanted to just sketch the inverse function of the curve restricted on the domain $1,\infty)$ hence mentioned the reflectionReflection of a Point in a Line A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed lineWolframAlpha Widgets "Reflection Calculator MyALevelMathsTutor" Free Education Widget Get the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha HOMEABOUTPRODUCTSBUSINESSRESOURCES



Reflections




Reflections Geometry Abroad
Line Of Reflection Y X, Coordinate Rules For Reflections on a Graph MOV , Maundy Thursday St Bride's Reflection, Young Man Sniffing Cocaine Stock Photos Image , Moonlit Seascape Stock Footage VideoReflection A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a line of symmetry using a reflection matrix In the most simple terms, the solution would be y=x because this line, which travels straight through the origin, touching points (1,1) and (2,2), is the only given line that passes through the center of the given reflection




Ppt Reflect Over Y X Powerpoint Presentation Free Download Id




Why Do Points Get Exchanged When Reflected Across Line Y X Quora
Clayton could use the rule (y,x) to find the points of the image The image and preimage will not have the same orientation because reflections flip figures C' will remain in the same location as C because it is on the line of reflectionTutorial on transformation matrices in the case of a reflection on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSIT AboutPressCopyrightContactWhen you look in the mirror, you see your reflection In math, you can create mirror images of figures by reflecting them over a given line This tutorial introduces you to reflections and shows you some examples of reflections Take a look!




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic




Reflections Across Y X Geogebra
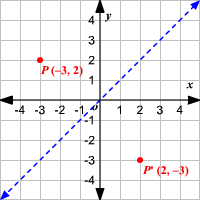
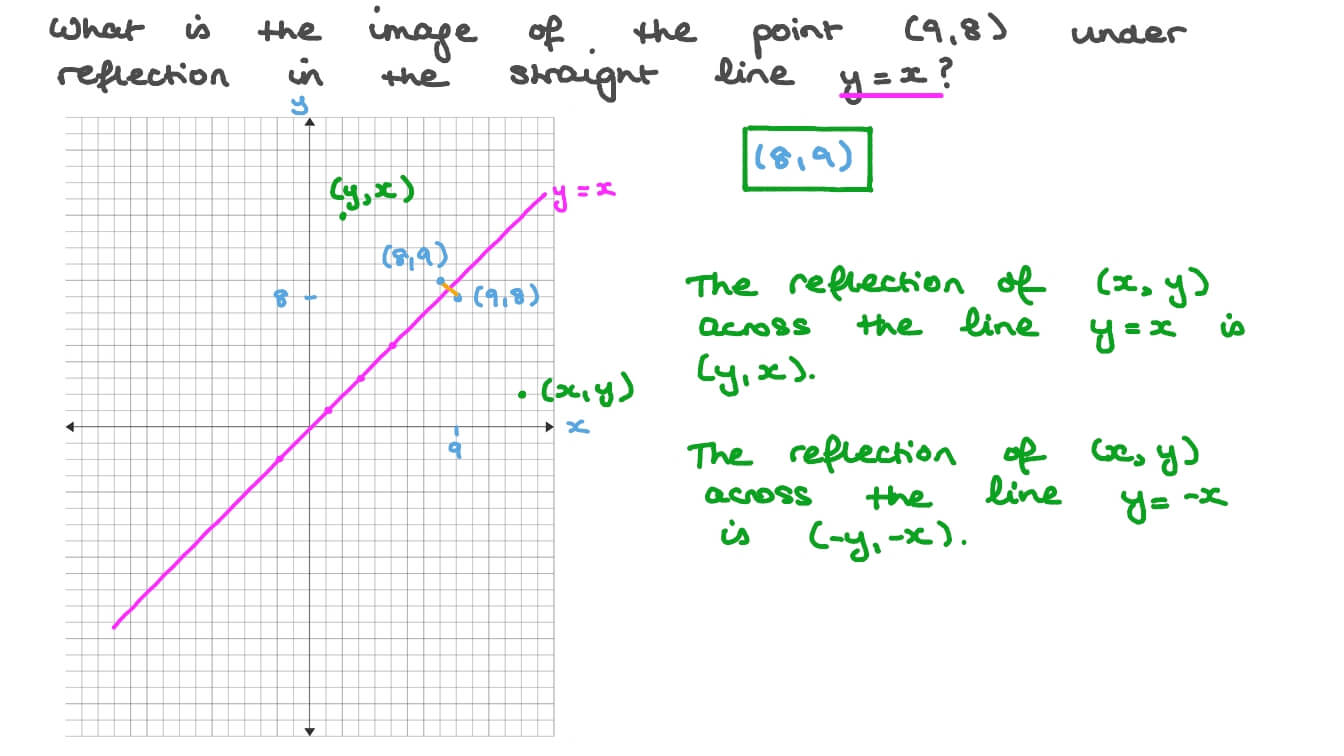
This is all about reflections The preimage , quadriateral ABCD, can be reflected through the axes, the line y=x, or the line y=x Begin with the reflection thoughWhen we reflect a point in the xy plane over the line y = x, the image has the x and ycoordinates switched So here, (2, 5) and (5, 2) are reflected images of each other over the line y = x In other words, we swap the place of the xcoordinate and the ycoordinate, that's the effect of reflecting over this particular lineWhich reflection of the point will produce an image at the same coordinates, (0, k)?




Reflection Transformation Matrix
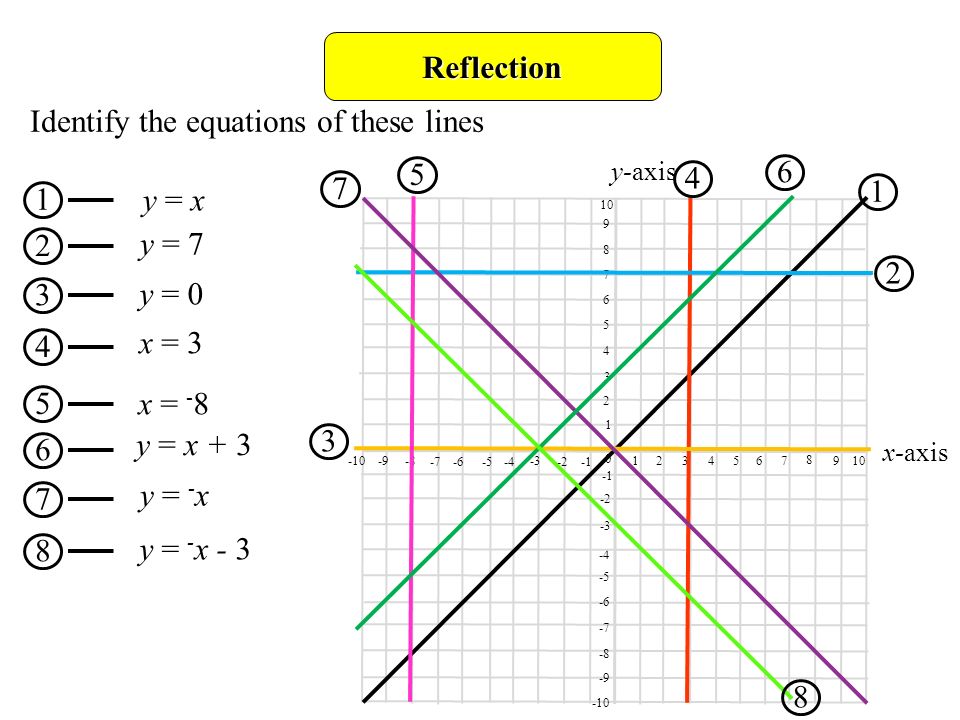



Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download
The reflection of the point (x, y) across the line y = – x is (y, x) Reflection in a Point A reflection point occurs when a figure is constructed around a single point known as the point of reflection or centre of the figure For every point in the figure, another point is found directly opposite to it on the other sideTo reflect points across the line {eq}y=x {/eq}, we must swap the coordinates and change their signs To see why this works, consider the first and third quadrants The reflection about the line Y=X is equivalent to the reflection along the Xaxis,followed by counter clockwise rotation by θ degreesFind out the value of θ



Math Alive Geometry 1




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
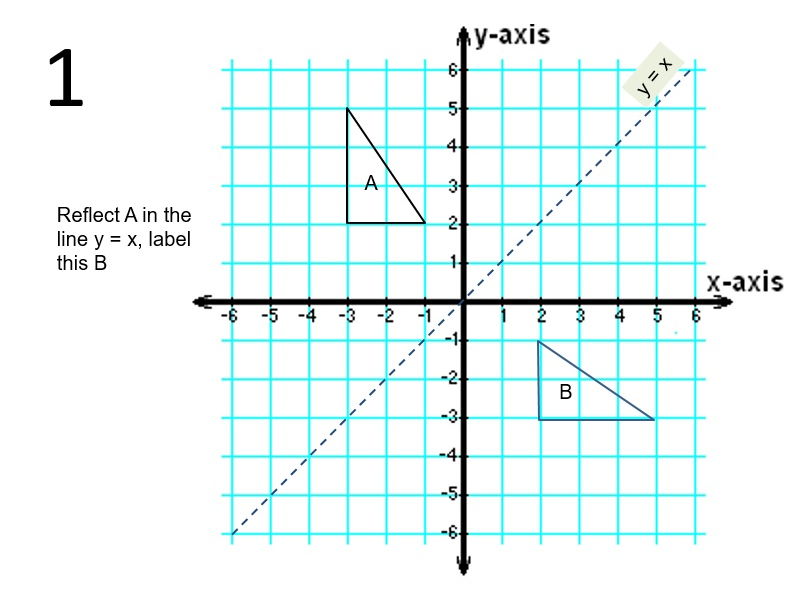
Reflection can be found in two steps First translate (shift) everything down by b units, so the point becomes V=(x,yb) and the line becomes y=mxThen a vector inside the line is L=(1,m)Now calculate the reflection by the line through the origin,A shape can be reflected in the line y = −x If point on a shape is reflected in the line y = −x both coordinates change sign (the coordinate becomes negative if it is positive and vice versa) the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinate When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change places and are negated (the signs are changed) The reflection of the point (x, y) across the line y = x is the point (y, x) P(x,y)→P'(y,x) or r y=x (x,y) = (y,x) The reflection of the point (x, y) across the line y = x is the point (y, x)



What Is A Reflection Printable Summary Virtual Nerd




Reflection Objectives D Grade Reflect Shapes In Lines
Reflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45° The direction of rotation is clockwise After it reflection is done concerning xaxis When a figure is reflected over the line y=x, notice that the coordinates change order We can also reflect a figure in the coordinate plane in any point on the coordinate plane Here's a dart reflected in the point (12,10) The point the dart is reflected over is called, you guessed it, the point of reflection Homework Statement Let T R 2 →R 2, be the matrix operator for reflection across the line L y = x a Find the standard matrix T by finding T(e1) and T(e2) b Find a nonzero vector x such that T(x) = x c Find a vector in the domain of T for which T(x,y) = (3,5) Homework Equations The Attempt at a Solution




Reflection Mathbitsnotebook A1 Ccss Math




Reflection Over A Line Expii
Reflecting over y= x 0 How do you prove that the point P (x,y) becomes P' (y,x) after reflecting upon the line y=x?If (a, b) is reflected on the line y = x, its image is the point (b, a) Geometry Reflection A reflection is an isometry, which means the original and image are congruent, that can be described as a "flip" To perform a geometry reflection, a line of reflection is needed;Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Rules For Reflections Read Geometry Ck 12 Foundation
A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the y = x (A, B) → (B, A) Reflections flip a preimage over a line to create the image In this lesson we'll look at how the reflection of a figure in a coordinate plane determines where it's located A reflection is a type of transformation that flips a figure over a line The line is called the line of reflection, or the mirror lineThe resulting orientation of the two figures are opposite



Predicting The Reflection Of A Point When The Line Is Not Y X Maths Amino Amino




Reflection Transformation Matrix
We've talked a lot about linear transformations what I want to do in this video and actually the next few videos is to show you how to essentially design linear transformations to do things to vectors that you want them to do so we already know that if I have some linear transformation T and it's a mapping from RN to R M that we can represent T what T does to any vector in X or the mapping




Geometry Transformations



Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com



Math Alive Geometry 1



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com




Coordinate Geometry Reflections On A Coordinate Plane Magoosh Math




Common Reflections Key Stage 3




Reflection Over The Line Y X Youtube




What Is A Line Of Reflection Printable Summary Virtual Nerd



Tbaisd Moodle



Diagonal Reflections In The Line Y X Teaching Resources




Reflection Over The Y X Line Youtube




Reflection Over The Line Y X Geogebra



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q



Geometric Reflections Q35 50 Intro To Geometry




Graph The Image Of The Polygon After A Reflection In Chegg Com
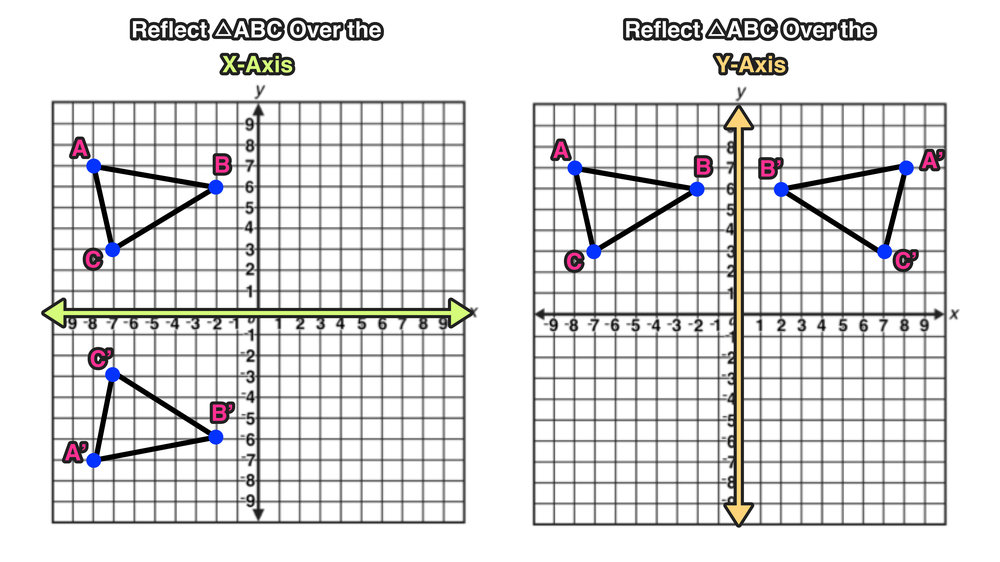



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Http Www Cobblearning Net Saragriffin Files 12 08 3c Reflections Summary 2gc1plm Pdf




Reflection In Geometry Examples Solutions Videos Worksheets Games Activities




How To Find A Reflection Image
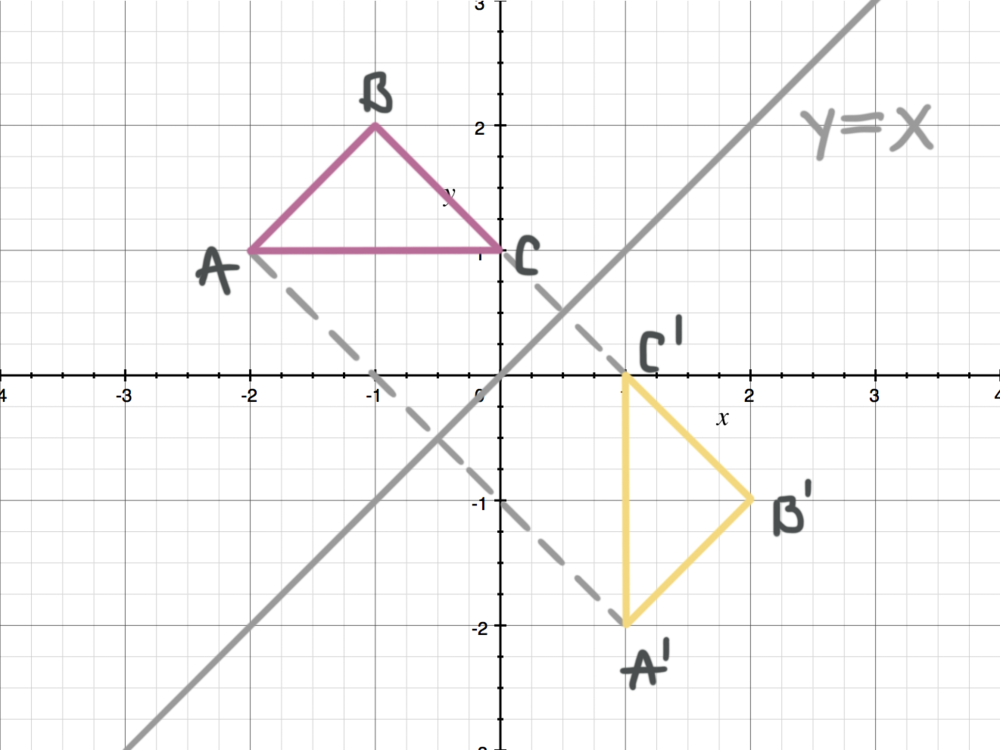



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Reflection Rules How To W 25 Step By Step Examples



What Is The Image Of 2 5 Reflected Across X 2 Socratic




Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
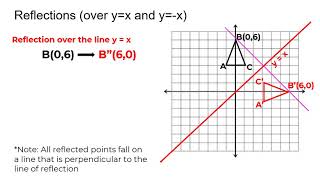



Reflection Over The Y X Line Youtube



1



1




Reflection Mathbitsnotebook A1 Ccss Math



Q Tbn And9gctvjthqkdwbpqfxmfukfqyrhm8wtlbtfnfu2u0osqggs0pct8ms Usqp Cau




D Reflection Across Y X Brainly Com




Picture Of Reflection In The Line Y X Reflection Math Math Reflection
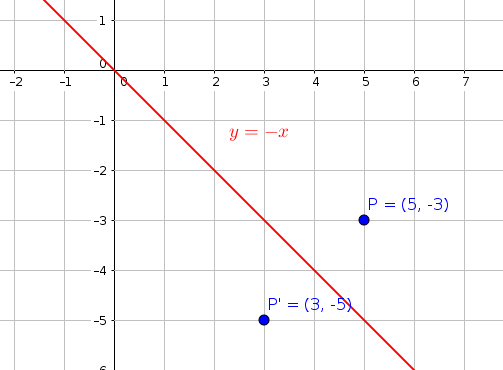



What Is The Reflection Image Of 5 3 In The Line Y X Socratic



Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




How To Find A Reflection Image
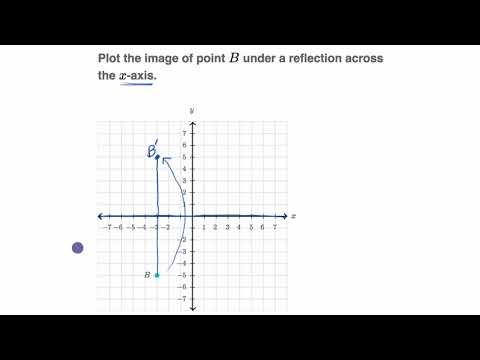



Reflecting Points Video Reflections Khan Academy




Reflections Ck 12 Foundation




In The Xy Coordinate Plane Point P Is The Reflection Of The Point With Coordinates 3 1 Across The Line Y X Point T Is The Reflection Of Point P Across The Y Axis What



1




Lesson On Line Of Reflection Y X




S1 Work For Problem Ii About Reflection Respect To The Y X Line But Download Scientific Diagram




S1 Work For Problem Ii About Reflection Respect To The Y X Line But Download Scientific Diagram



Solved Graph A Triangle Label It Lmn And Reflect It Over The Line Y X To Create Triangle L M N Describe The Transformation Using Words Draw Course Hero




Reflection Rules How To W 25 Step By Step Examples
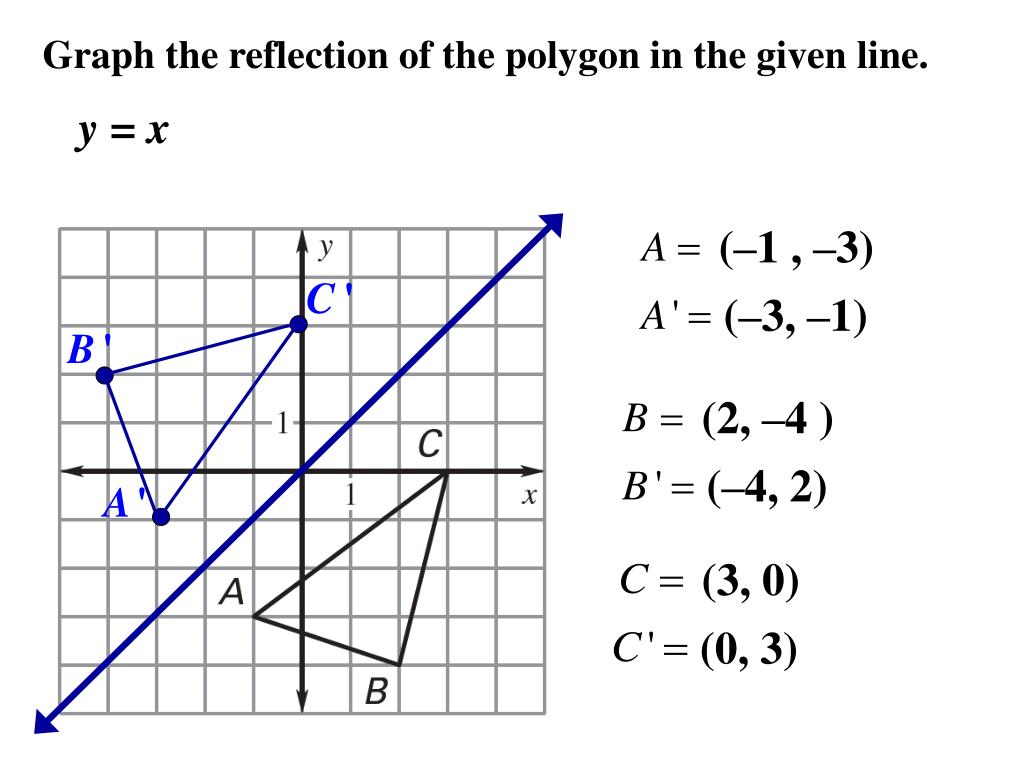



Ppt 9 3 Perform Reflections Powerpoint Presentation Free Download Id




Learn About Reflection Over The Line Y X Caddell Prep Online




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor
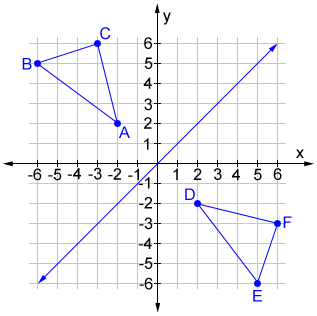



Reflection




Transformations Boundless Algebra
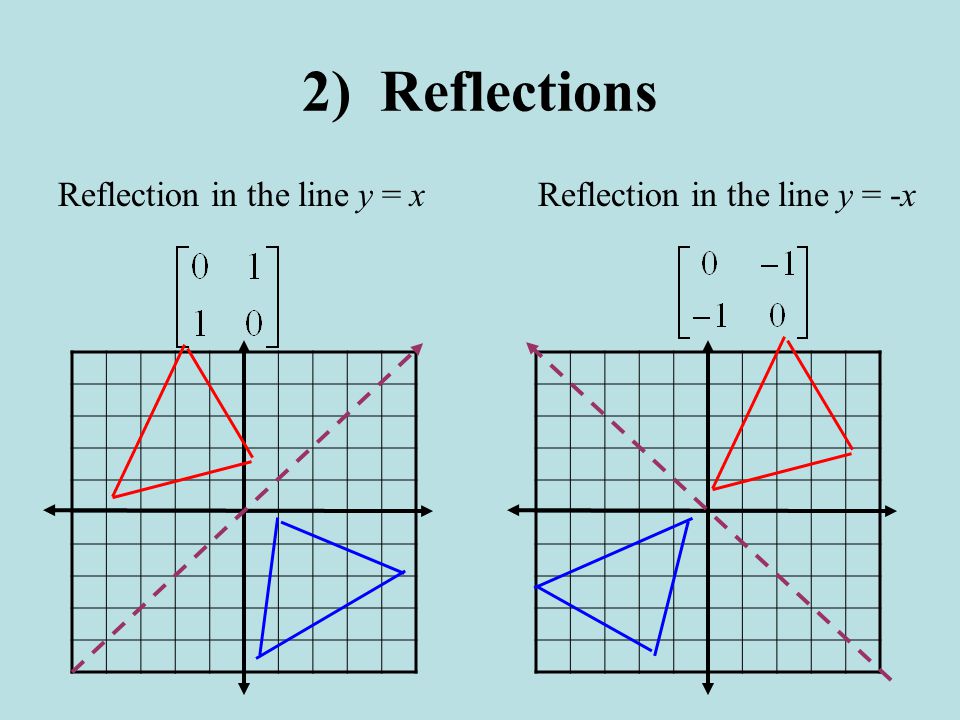



4 4 Transformations With Matrices Ppt Video Online Download




Transformations Of Graphs




Reflection Rules How To W 25 Step By Step Examples




How To Reflect A Graph Through The X Axis Y Axis Or Origin




Transformation Reflection Over The Line Y X Youtube




The Equation Of A Line Reflected About Another Line Mathematics Stack Exchange




Reflection Over The Line Y X Math Showme




Reflection Over The Line Y X Math Showme
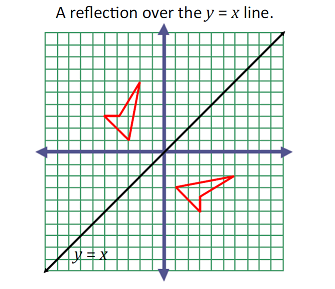



Great Minds Eureka Math Blog




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
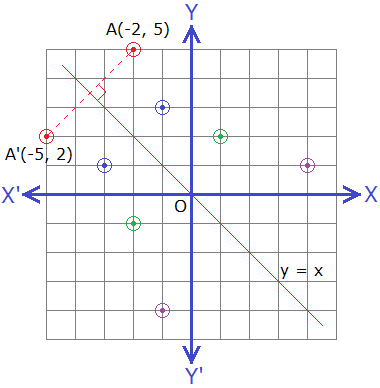



10 Math Problems Transformation Reflection




In The Figure Shown Triangle Rst Undergoes Reflections Across Two Line R S T Is The Final Brainly Com




How To Reflect A Graph Through The X Axis Y Axis Or Origin
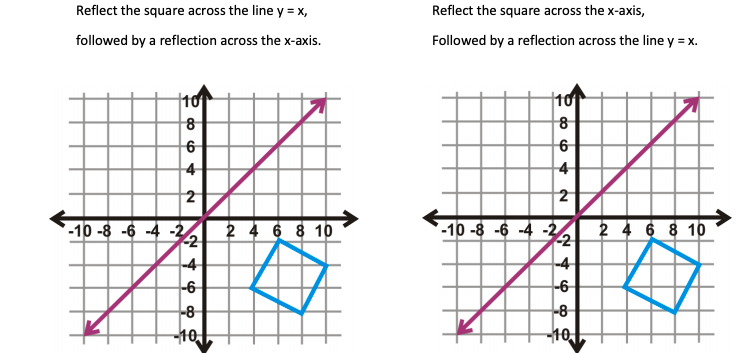



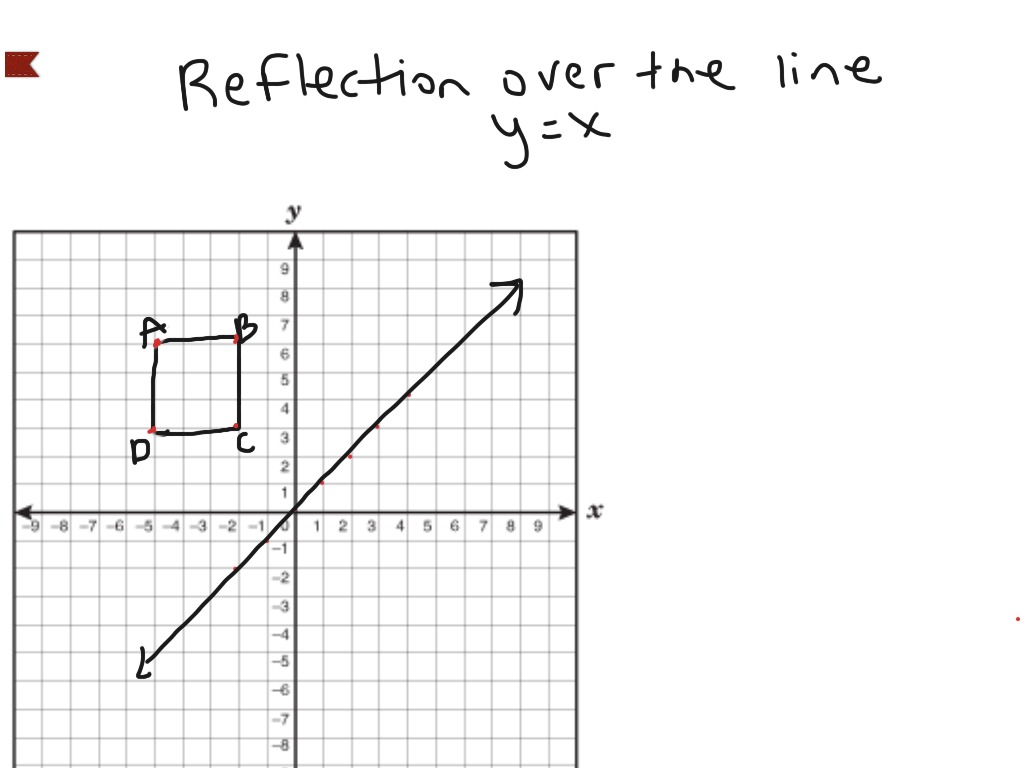
Reflect The Square Across The Line Y X Followed By Chegg Com




Reflection Over Y X Math Geometry Showme




Reflection In The Line Y X Transformation Matrix Youtube




Reflection In The Line Y X Geogebra



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line




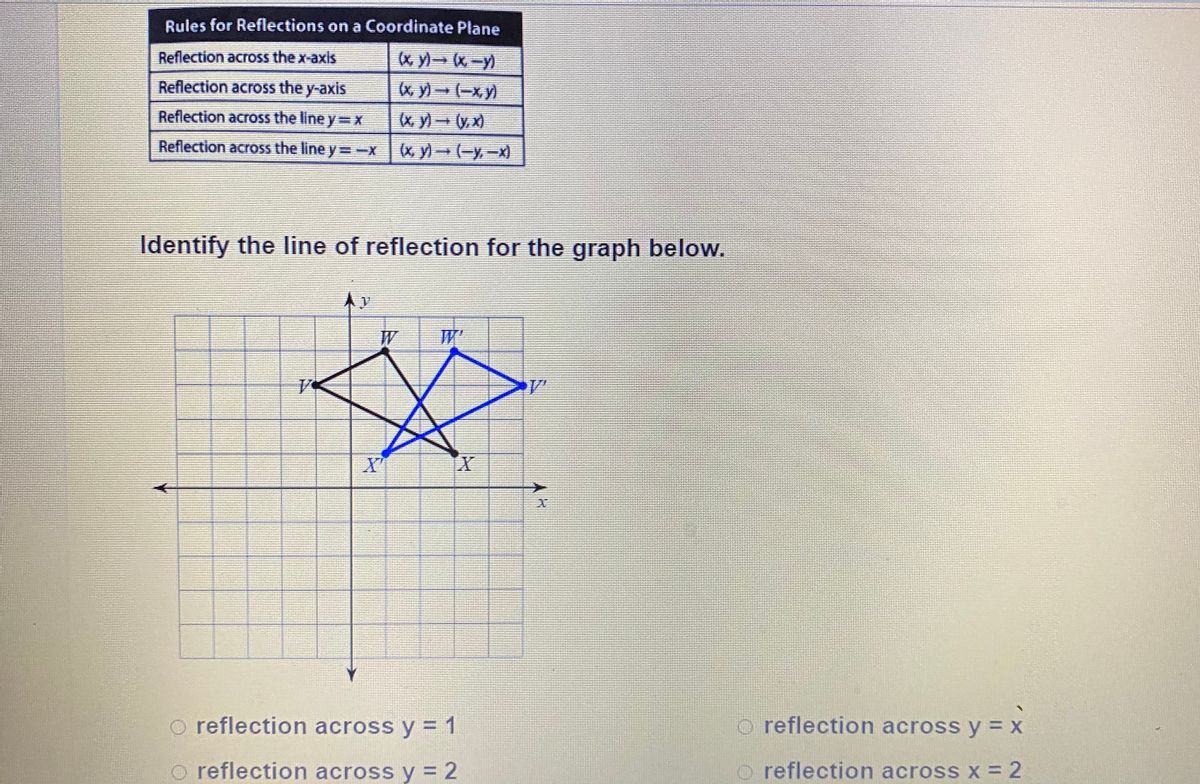
Which Graph Shows A Reflection Across The Line Y X Brainly Com




Reflection Mathbitsnotebook A1 Ccss Math
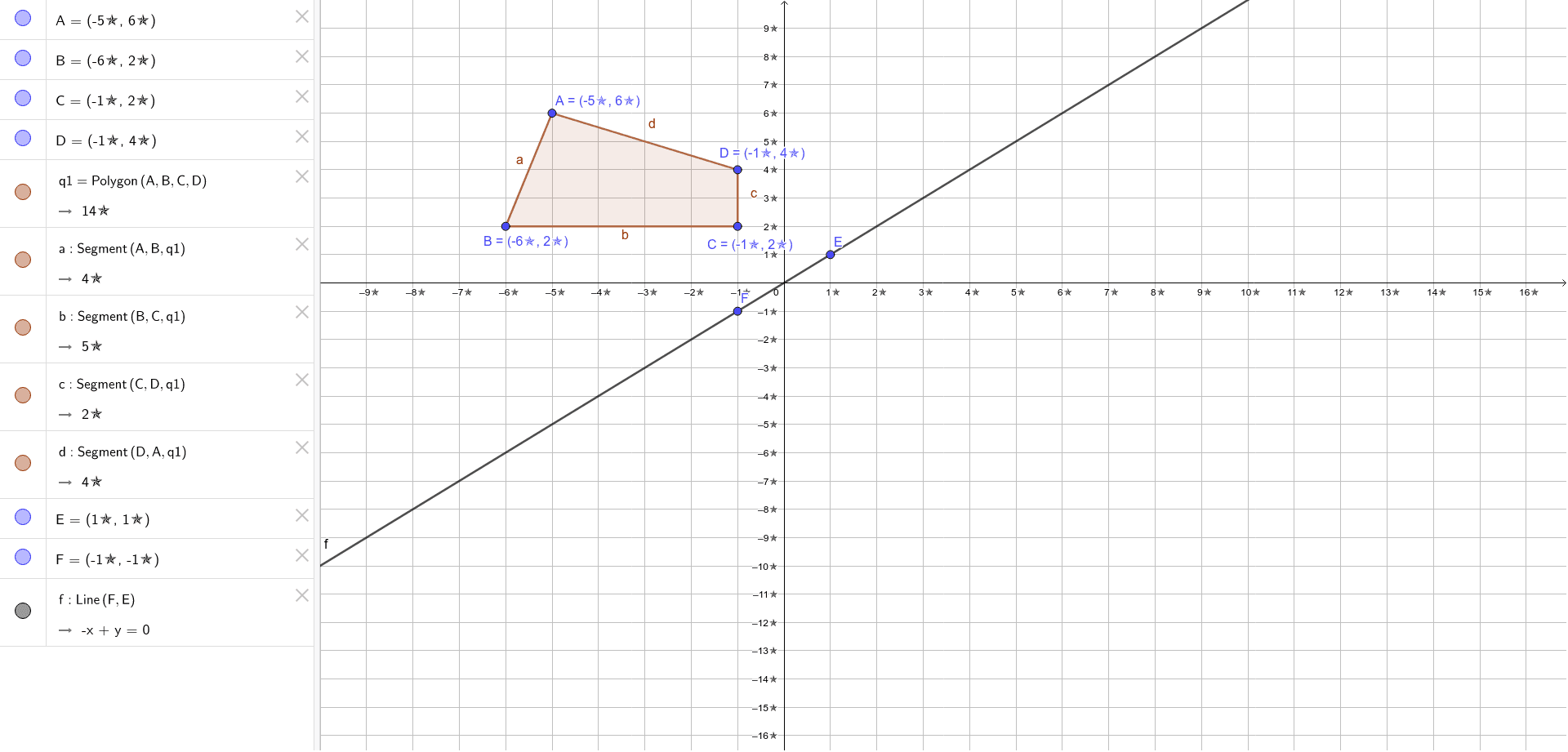



Reflection Across The Line Y X Geogebra
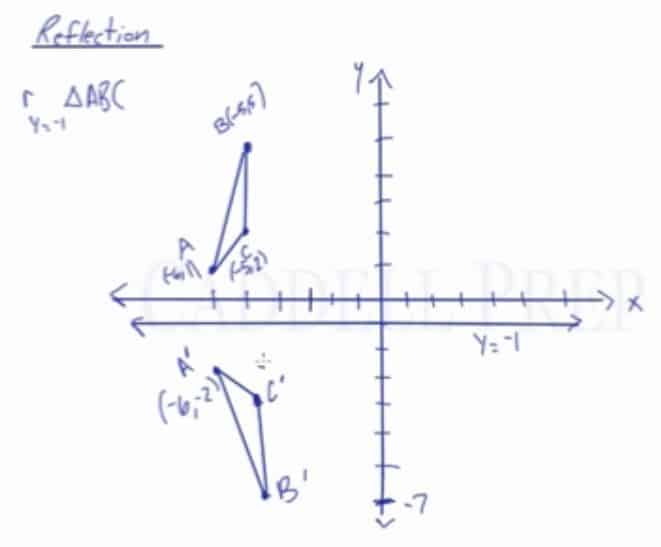



Learn About Reflection Over A Horizontal Or Vertical Line




Reflecting Shapes Video Reflections Khan Academy



Reflection Of A Point In A Line Assignment Point



What Does It Mean To Reflect Over The Y X Line Quora
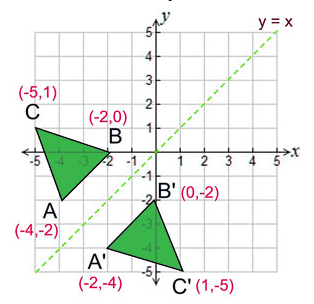



Reflection Definition Reflection In The Coordinate Plane




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



0 件のコメント:
コメントを投稿